Cálculo de Confiabilidad para una familia de equipos
Este artículo lo he querido escribir a solicitud de algunas personas que han visitado mi página y quieren profundizar en el tema del «Análisis y Tratamiento de Datos para el Estudio de la Confiabilidad de Equipos».
Antes de iniciar con este tema quiero indicarles que un estudio de confiabilidad lo podemos hacer para un equipo o para una cantidad de equipos de una misma familia, con esto quiero significar, de iguales características técnicas. Obviamente no podemos hacer un análisis con una mezcla de peras con manzanas. Me refiero a que todas las fallas son paradas , pero no todas las paradas son fallas.
UN EJEMPLO DE CÁLCULO DE CONFIABILIDAD
Una parada por mantenimiento preventivo no es una falla. Una parada administrativa u operativa tampoco son fallas. Un cuidado hay que tener con este otro escenario que es: cuando tengamos diferentes tipos de fallas para los mismos equipos. En los siguientes párrafos profundizaremos esta parte.
Es importante que sepamos que podemos analizar una data cuyos equipos de iguales características han fallado todos durante un tiempo de corrida o simplemente han fallado cierta cantidad de ellos.
¿QUÉ ES LA CONFIABILIDAD EN MANTENIMIENTO?
Primero definamos la Confiabilidad de un equipo como la Probabilidad que tiene éste de no de fallas durante un tiempo (t).
Mas adelante en las próximos párrafos la formularemos. Regresando a lo anteriormente dicho, cuando analizamos los tiempos de fallas de los equipos y todos ellos han fallado, decimos que la «Data es Completa», caso contrario que han fallado algunos de ellos y otros siguen operando, decimos que la «Data es Incompleta o Censurada”. Recuerden que estamos hablando de una familia de equipos y no de un solo equipo.

Para que entremos en detalle, y entendamos cómo se debería procesar y analizar manualmente una data, vamos a proceder con una corrida de ventiladores de generadores diesel para la cual la alta gerencia desea saber si esas fallas corresponde a fallas pobres o fallas que podrían tipificarse como tempranas en la vida de los ventiladores, o son fallas que están dentro del rango normal de operaciones, o simplemente, son fallas reiterativas y continuas que aparecen cuando la vida útil de estos ventiladores está llegando a su final y es cuando comienzan a presentarse éstas producto de un incremento acelerado de la rata de fallas.
En la TABLA I encontramos los valores de los instantes de fallas por cada ventilador de motores Diesel y los que aún se mantienen vivos u operando. En la columna (#) tenemos la cantidad de los ventiladores, en total setenta (70). En la columna 2, vamos a colocar el inverso de esta numeración. De igual manera, tenemos en la columna 3 el instante de falla en horas de cada ventilador multiplicado por 100 para obtener el porcentaje (Hazard Values). Y en la última columna vamos a colocar la frecuencia acumulada, que de aquí en adelante llamaremos la Función Acumulada de Riesgo (Cumulative Hazard). Para que es importante esta última columna de la función de Riesgo Acumulada. Ésta es la que nos va a permitir plotear los valores en los papeles funcionales de Weibull.
TABLA 1
| # | Orden inverso | data observada en horas | 100*valores de riesgo | valor de riesgo acumulado =(frecuencia acumulada) |
| 1 | 70 | 4500* | 1,43 | 1,43 |
| 2 | 69 | 4600 | ||
| 3 | 68 | 11500* | 1,47 | 2,9 |
| 4 | 67 | 11500* | 1,49 | 4,39 |
| 5 | 66 | 15600 | ||
| 6 | 65 | 16000* | 1,54 | 5,93 |
| 7 | 64 | 16600 | ||
| 8 | 63 | 18500 | ||
| 9 | 62 | 18500 | ||
| 10 | 61 | 18500 | ||
| 11 | 60 | 18500 | ||
| 12 | 59 | 18500 | ||
| 13 | 58 | 20300 | ||
| 14 | 57 | 20300 | ||
| 15 | 56 | 20300 | ||
| 16 | 55 | 20700* | 1,82 | 7,75 |
| 17 | 54 | 20700* | 1,85 | 9,60 |
| 18 | 53 | 20800* | 1,89 | 11,49 |
| 19 | 52 | 22000 | ||
| 20 | 51 | 30000 | ||
| 21 | 50 | 30000 | ||
| 22 | 49 | 30000 | ||
| 23 | 48 | 30000 | ||
| 24 | 47 | 31000* | 2,13 | 13,62 |
| 25 | 46 | 32000 | ||
| 26 | 45 | 34500* | 2,22 | 15,84 |
| 27 | 44 | 37500 | ||
| 28 | 43 | 37500 | ||
| 29 | 42 | 41500 | ||
| 30 | 41 | 41500 | ||
| 31 | 40 | 41500 | ||
| 32 | 39 | 41500 | ||
| 33 | 38 | 43000 | ||
| 34 | 37 | 43000 | ||
| 35 | 36 | 43000 | ||
| 36 | 35 | 43000 | ||
| 37 | 34 | 46000* | 2,94 | 18,78 |
| 38 | 33 | 48500 | ||
| 39 | 32 | 48500 | ||
| 40 | 31 | 48500 | ||
| 41 | 30 | 48500 | ||
| 42 | 29 | 50000 | ||
| 43 | 28 | 50000 | ||
| 44 | 27 | 50000 | ||
| 45 | 26 | 61000 | ||
| 46 | 25 | 61000* | 4,00 | 22,78 |
| 47 | 24 | 61000 | ||
| 48 | 23 | 61000 | ||
| 49 | 22 | 63000 | ||
| 50 | 21 | 64500 | ||
| 51 | 20 | 64500 | ||
| 52 | 19 | 67000 | ||
| 53 | 18 | 74500 | ||
| 54 | 17 | 78000 | ||
| 55 | 16 | 78000 | ||
| 56 | 15 | 81000 | ||
| 57 | 14 | 81000 | ||
| 58 | 13 | 82000 | ||
| 59 | 12 | 85000 | ||
| 60 | 11 | 85000 | ||
| 61 | 10 | 85000 | ||
| 62 | 9 | 87500* | 12,5 | 35,28 |
| 63 | 8 | 87500 | ||
| 64 | 7 | 87500 | ||
| 65 | 6 | 94000 | ||
| 66 | 5 | 99000 | ||
| 67 | 4 | 101000 | ||
| 68 | 3 | 101000 | ||
| 69 | 2 | 101000 | ||
| 70 | 1 | 115000 |
La suma de las horas: 3.444.400 horas
Los valores con (*) corresponden a los instantes de fallas de los generadores por causa de ventiladores. Para plotear esta función con los valores (*) lo haremos en el papel funcional logarítmico de dos ciclos o de tres ciclos según sea el caso, tal como se muestra en dichos papeles que a continuación se presenta.
CÁLCULO DE CONFIABILIDAD SEGÚN EL PAPEL DE WEIBULL DE DOS CICLOS LOGARÍTMICOS
CÁLCULO DE CONFIABILIDAD SEGUN EL PAPEL DE WEIBULL DE TRES CICLOS LOGARÍTMICOS

INTERPRETACIÓN DE GRÁFICAS PARA EL CÁLCULO DE LA CONFIABILIDAD
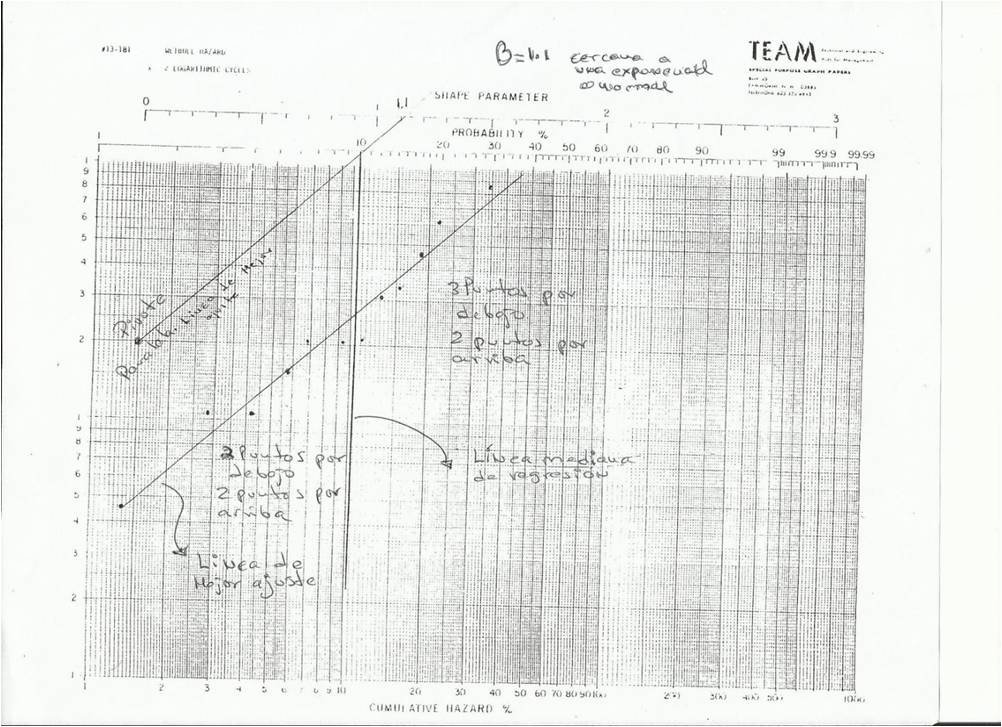
Observemos que en el lado de los valores X encontramos la Función de Riesgo Acumulada, que es indicado en la cuarta columna de la TABLA I. En el lado de los valores Y, encontramos los dos ciclos del papel logarítmico, donde colocaremos los instantes de fallas en horas de cada ventilador. La Gráfica se muestra de la siguiente manera con los valores ploteados. El primer punto indicado corresponde a la intersección de 4.500 horas con 1,43. El segundo punto corresponde a la intersección de 11.500 horas con 2.90 de la Función Acumulada de Riesgo. El tercer punto corresponde a la intersección de 11.500 horas con el valor acumulado de 4,39 de la Función de Riesgo Acumulada, y así sucesivamente para las demás intersecciones hasta el último valor que corresponde la 87.500 horas con 35,28.
Una vez ploteados todos los valores, trazamos la recta dejando la misma cantidad de puntos por arriba que por debajo. Lo interesante de usar los papeles Weibull es porque según el parámetro de forma (ß) podemos saber cuál distribución está gobernando el comportamiento del equipo o equipos. Razón por la cual se dice jocosamente que esta distribución Weibull es travesti , porque puede pasar de un lado de distribución a otro dependiendo del parámetro de forma.
Cómo iniciamos
- Trace la línea de mejor ajuste, dejando la misma cantidad de puntos arriba que debajo de la línea.
- Levante la línea vertical o la mediana de los valores. Esta mediana divide en partes iguales los puntos a la izquierda y a la derecha. Ésta se llama también en inglés (Median Regresssion line). Recuerden que solo en la distribución normal la media es igual a la mediana e igual a la moda
- Intercepte esta media con una PARALELA a Línea de Mejor ajuste hasta el punto pivote u origen. Con esta intersección leemos el valor de BETA (ß) Parámetro de Forma (Shape Parameter). Muchos han escuchado la famosa curva de la bañera y su relación con el parámetro ß.
Veamos cómo queda la gráfica de Mejor Ajuste
- ß<1 los equipos están en mortalidad infantil la rata de falla decrece (ley poisson)
- ß=1 los equipos están operación normal (ley exponencial o uniforme)
- ß≤3 los equipos comienzan a degradarse envejecimiento (ley log-normal)
- ß>3 los equipos continúan degradándose, envejecimiento acelerado (ley normal)
Ahora bien, como podemos observar el punto de corte corresponde a un ß=1,1, está alrededor de 1. En consecuencia la situación de los ventiladores podemos decir que esta presencia de fallas está dentro de su operación normal. Si durante una corrida vemos que podemos trazar una línea recta, decimos que el papel usado fue acertado, en caso contrario no se puede trazar una recta debemos usar otros tipos de papeles para linealizar los valores, que es la función principal de estos papeles funcionales.
Fíjense que al tener una distribución exponencial la rata de fallas es igual a: λ=1/θ y donde el estimador θ=1/MTBF. La rata de falla λ siempre viene expresada en unidad de tiempo: una (1) hora, mil horas, etc.
FORMULA PARA EL CÁLCULO DE LA CONFIABILIDAD

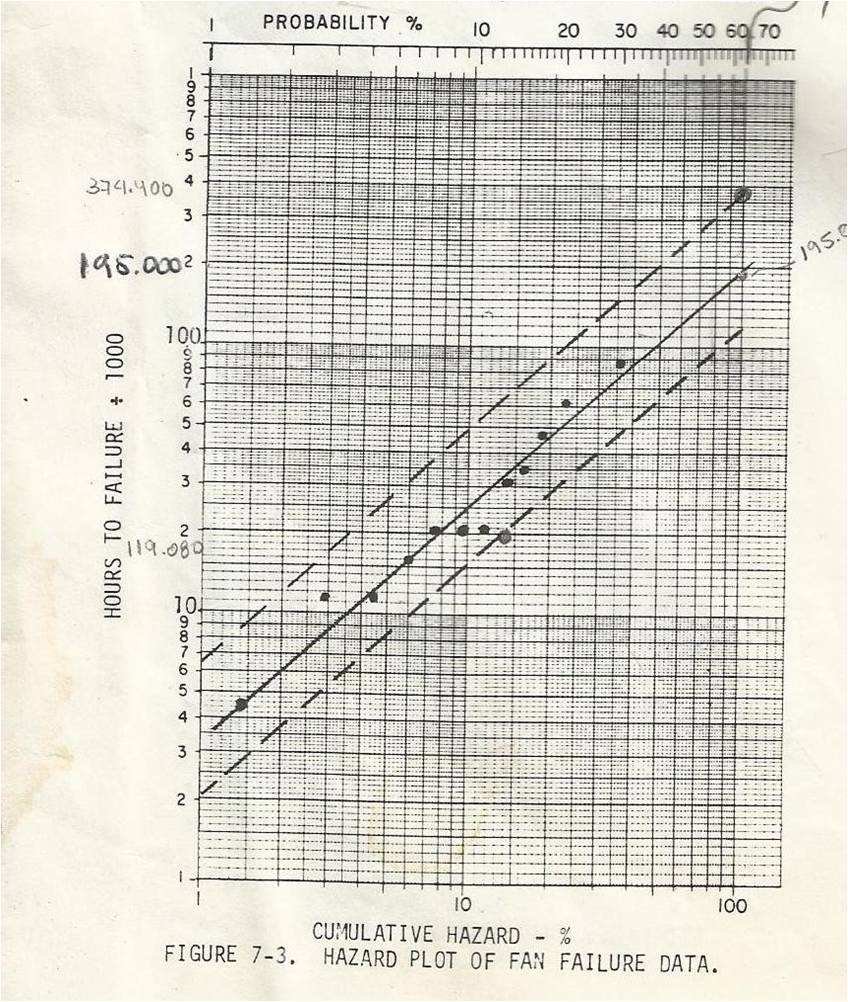
Para calcular la Rata de Fallas (λ) tenemos que identificar el mejor estimador para una distribución exponencial. Para ello utilizaremos el Papel Weibull de tres ciclos logarítmicos. La interpretación usada para este papel indica que el mejor estimador (Θ) ocurre al 100 % de del valor de la función Acumulada de Riesgo o también al 63 % de la Probabilidad de Falla Acumulada (ver gráfica siguiente). Para el caso que nos ocupa este valor está muy cercano a las 195.000 horas. De igual manera como ploteamos los valores en el papel Weibull de dos ciclos, debemos hacerlo con el de tres ciclos para conseguir este valor. Fíjense que deben correrse la escala, porque ahora están trabajando con tres ciclos.
VALIDEZ Y CONFIABILIDAD DE INSTRUMENTOS DE EVALUACIÓN Y DE INVESTIGACIÓN
Luego λ= (1×100)/( θ/1000)
= 100/(195.000/1000)
= 0,51% /1000 horas
Otro método para la calcular el (θ) analíticamente es el siguiente:
Θ=∑horas/ # de fallas, esto es igual a:
Θ=3.444.400/12= 287.000 horas.
Como podemos ver, este valor es casi el doble del estimador calculado gráficamente. Aquí surge una disyuntiva ¿Cuál es el correcto? Este problemas tenemos que resolverlo estadísticamente a través de los intervalos de confianza para ambos estimadores de la manera siguiente:
Фi= Θ (2F/X²(L:F)= límite inferior
Фs= Θ (2F/X²(U:F)=Límite superior
Donde Ф= es el estimador de la media de tiempo de falla. Y con relación a los limites utilizaremos un Chi cuadrado X².
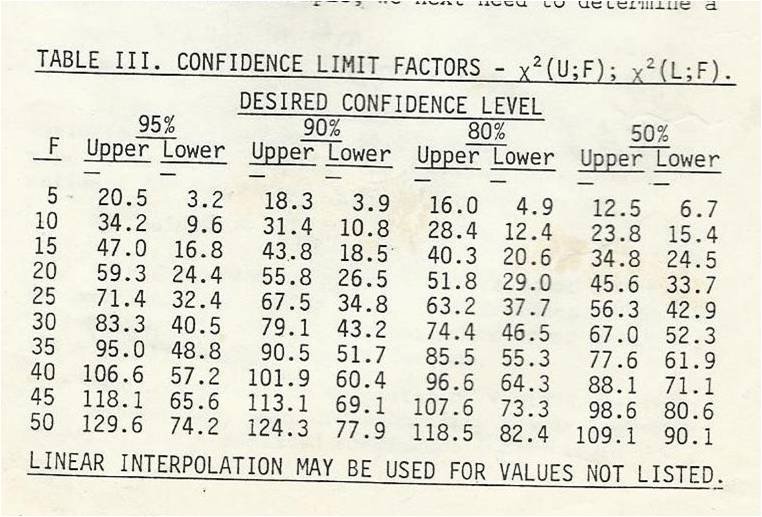
Es importante que para valores de número de fallas que no aparecen en la tabla, podemos perfectamente interpolar para conseguir los valores de cantidad de fallas.
Calculando estos intervalos de confianza para una Chi cuadrado X² con un nivel de confianza del 95 %, los límites son como siguen:
U=34,2 + (2/5(47,0 – 34,2)= 39,3
L=9,6 + (2/5(16,8 – 9,6)= 12,5
Фi= 195.000(2×12/12,5)=374.400 y se colocan en la gráfica
Фs= 195.000(2×12/39,3)=119.080 y se colocan en la gráfica
Tranzando las paralelas a la recta de mejor ajuste y que corten los valores de límites superior e inferior en el eje (Y) tenemos en la gráfica el siguiente resultado
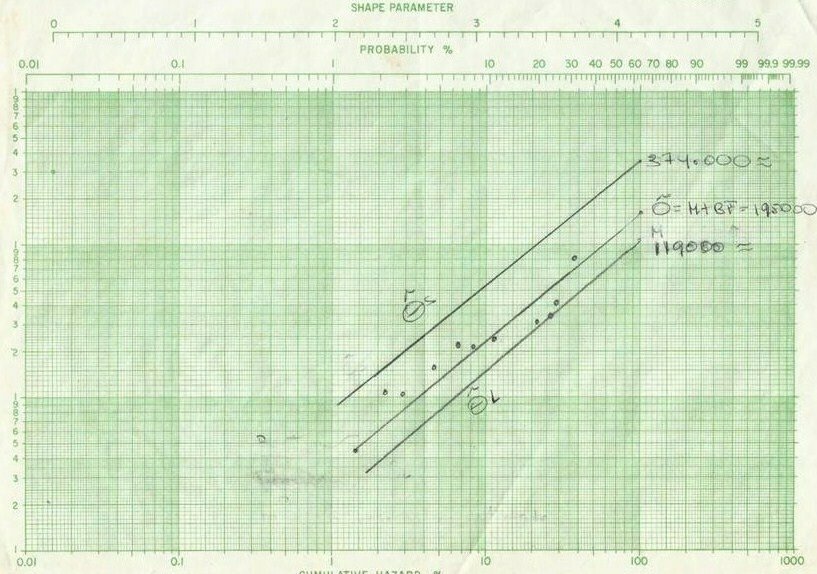
Ahora bien para el estimador de máximo verosimilitud para los valores U y L del cálculo analítico tenemos lo siguiente:
Фi= 287.000(2×12/12,5)=551.040
Фs= 287.000(2×12/39,3)=119.080
¿Qué significan estos valores, que para ambos casos podemos decir que el mejor estimador se encuentra entre esos intervalos de confianza con una nivel de confianza del 95 %. Importante está malo decir que el mejor estimador se puede asegurar con un nivel de confianza del 95 % que el valor de 287.000.
NOTA:
Para la segunda entrega calcularemos la confiabilidad para un equipo a través de La Distribución de Weibull

¿CÓMO HACER UN CÁLCULO DE CONFIABILIDAD?, OTRO EJEMPLO A DESARROLLAR
Es importante antes de comenzar este segundo ejercicio, sugiero familiarizarse con lo anterior explicado. En esta segunda vamos a escribir sobre el cálculo de confiabilidad para un equipo. Lo haremos de una manera gráfica, aunque existen muchos software de mantenimiento que realizan estos cálculos mucho mas rápido y con mayor exactitud, lo desarrollaremos de esta manera para fácil comprensión.
Para iniciar, tenemos en la Tabla T-1 la corrida de paradas por fallas de un equipo. Recuerden lo que hemos hablado en los artículos anteriores sobre que un mantenimiento de calidad necesita de mucho orden, disciplina, control y seguimiento. Es imposible realizar una corrida si no hay un seguimiento continuo a la operación de los equipos críticos.

Esto es: Arranque y Parada y su causa; y además, si no tenemos a la mano un «cuenta hora» u Horometro. Estos vienen colocados generalmente a equipos mecánicos o electromecánicos y son utilizados para controlar las intervenciones de mantenimiento preventivo de los equipos y junto con el detalle de cada interrupción, para el seguimiento del comportamiento de las fallas del equipamiento. En un Horómetro su conteo puede ser en Horas, Minutos y hasta segundos, dependiendo de lo sofisticado que éstos sean; y pueden ser programables o no; electromecánicos o electrónicos. De allí cuando en las lecturas encontramos valores con (coma) son horas mas minutos. Recuerden que las horas las expresamos en: Una hora es igual a una unidad de medida. Significa que media hora (0,30 minutos) su equivalente es 0,50, tal como lo vemos en los instantes de fallas en la Tabla T-1 que a continuación presento.
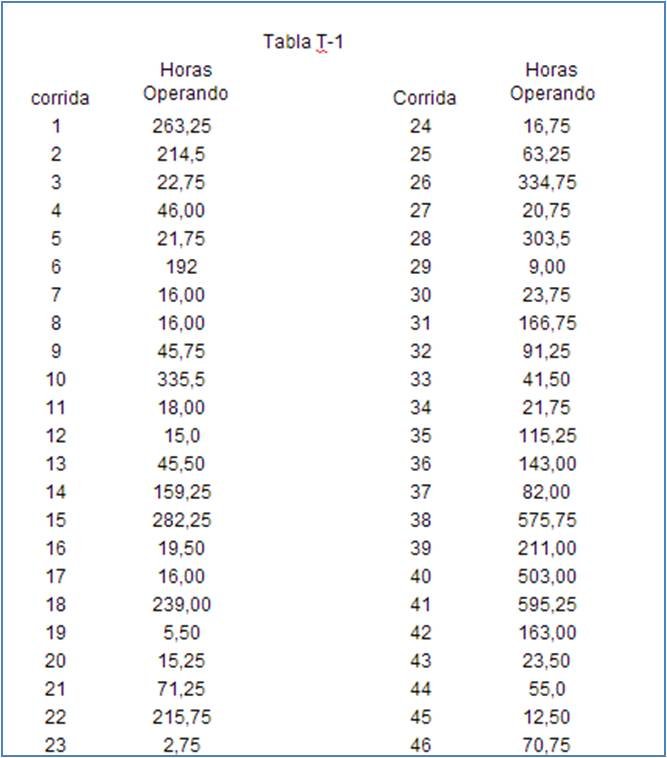
Lo primero que tenemos que hacer, tal como lo hicimos en la primera parte de este artículo y según el papel logarítmico que utilicemos, podemos trabajar con lo función de riesgo, lo vemos mas adelante. Procedamos a ordenar los valores de menor a mayor con el correspondiente instante de fallas para obtener de aquí en adelante los siguientes valores:
Ps(t): que es la probabilidad de que un equipo no falle cuando está en servicio durante un tiempo determinado. En otras palabras en la capacidad que tiene un equipo de no fallar en operación. El término Probabilidad de Supervivencia Ps (t) es sinónimo de Confiabilidad.

Ahora bien lo opuesto a Confiabilidad es Desconfiabilidad Pf(t), en consecuencia, el término Pf es sinónimo de Desconfiabilidad. Obviamente como son probabilidades
Pf(t) + Ps(t)=1
Esto se debe a que un equipo estará en una de las dos condiciones falla o en operación. Asumiendo que un equipo no está en servicio, pero tampoco está en falla, entonces decimos que está Disponible. Es por ello, que como lo comentamos en el la parte superior de este ejercicio, todas las fallas son paradas mas no todas las paradas son fallas, debido que también existen interrupciones por mantenimiento preventivo, paradas administrativas u operativas y ninguna de ellas es una falla.
Introduzcamos un nuevo término y es la rata de falla λ(t) y es la probabilidad de falla de un equipo después de T horas de operación, cuando sabemos que el equipo ha sobrevivido T-e horas, en donde e es el infinitésimo de tiempo. El estudio de Confiabilidad es el estudio de las fallas de los equipos, o sea, de la rata de falla λ(t). El número de horas transcurridas entre fallas es una medida de confiabilidad del equipo. En general se usan también los siguientes parámetros:
- TPEP: Tiempo Promedio entre fallas o también en inglés MTBR (Mean Time Between Failure)
- TPEP: Tiempo Promedio para Reparar o también en inglés MTTR (Mean Time to Repair)
- TPEP: Tiempo Promedio entre Paradas
En este parte vamos de igual manera a introducir la fórmula para el cálculo de Probabilidad de Supervivencia de equipos
ß
[-( t \ V ) ]
Ps(t)=е
Veamos aquí los dos parámetros de importancia V y ß, donde V significa la edad característica para fallar y mientras mas grande sea este valor, mejor es la confiabilidad del equipo. El valor ß mide la dispersión y por consiguiente la función de probabilidad o distribución que gobierna lel comportamiento de las fallas del equipo. Tal como lo indicamos en la Entrega # 1. Es de hacer notar que cuando ß=1 la distribución es exponencial, ya que
1
[-( t \ V ) ]
Ps(t)= е
y haciendo 1\V= rata de falla, tenemos
-(λt)
Ps(t)=е
que corresponde a la fórmula de una distribución exponencial
Regresando a la Tabla T-1 y ordenando los valores de menor a mayor y la posición que ocupa cada dato lo llamaremos Rango, De esta manera, obtenemos
Rango
Ps(t)= Rango/N+1, usamos N+1 para rangos pequeño. En este caso es 47.
Para valores N>100, usamos:
Ps(f)= Rango/N
Entonces
Pf(t) + Ps(t)=1
Aplicando esta fórmula a los valores de la tabla, ésta queda de la siguiente manera
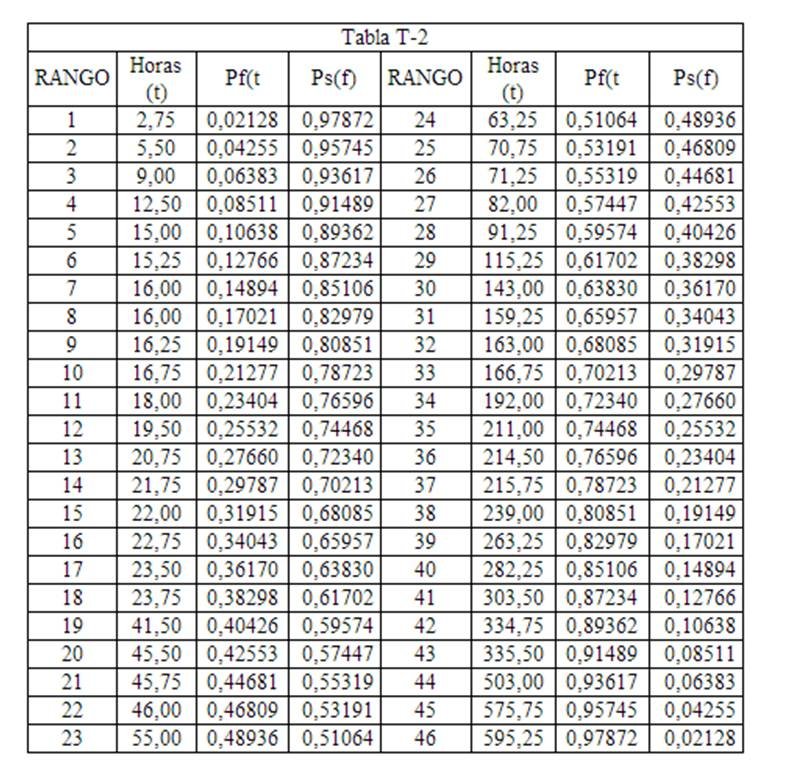
De igual manera procedemos a plotear en el papel logarítmico Weibull estos valores.
- Trazamos la línea de mejor ajuste que contenga la mayor cantidad de puntos, dejando la misma cantidad de puntos por arriba que por debajo. Fíjense que aún cuando hay 46 instantes de fallas, en el papel sólo tenemos 31 puntos colocados, esto es porque hay valores que casi se superponen, o simplemente, están superpuestos.
- Levantamos la Median Regresión Lineal dejando en la recta la misma cantidad de puntos tanto a la izquierda como a la derecha, tal como se muestra en la gráfica (Punto A). Fíjense que hay seis puntos muy alejado de la recta. Por lo tanto tenemos doce puntos a la izquierda del punto A y doce a la derecha del punto A. El valor de la Probabilidad de Supervivencia está entre 30 y 40 %. Y a la izquierda del punto a, obtenemos el valor aproximado de V= 115 horas.
- Por el punto pivote u origen (S) del papel que corresponde a la intersección (0,01;10 ), trazamos una paralela a la línea de mejor ajuste y prolongamos ésta hasta donde corta el valor del parámetro de forma K que para efecto nuestro es el valor ß de 0,79 cercano a 0.80.
- La ecuación de Confiabilidad queda de la siguiente manera y su gráfica de ilustra en la entrada de este artículo:
ß
[-( t \ V ) ]
Ps(t)=е
Sustituyendo
0,80
[ -( t \ 115 ) ]
Ps(t)=е
De ahora en adelante podemos calcular la probabilidad de supervivencia para cualquier tiempo (t) tan sólo sustituyendo el valor de t en la ecuación

![]()

